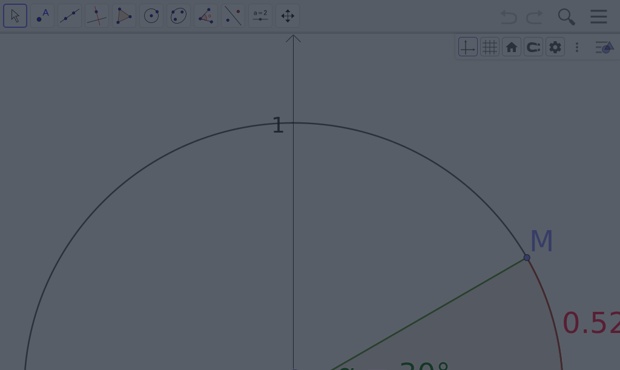
Mesurer un angle en radians

Dans un repère orthonormé, on considère le cercle de centre \(O\) et de rayon \(R=1\). Sa circonférence est égale à \(2\pi\).

On considère un point \(M\) sur le cercle. L'arc \(\small\overset{\frown}{AM}\) "s'enroule" autour du cercle dans le sens positif (sens inverse des aiguilles d'une montre).

On peut mesurer l'angle \(\small\widehat{AOM}\) par la distance parcourue par le point \(M\) sur le cercle (longueur de l'arc).

La longueur de l'arc \(\small\overset{\frown}{AM}\) est la mesure de l'angle \(\small\widehat{AOM}\) en radians.

Exemples

• La mesure en radians d'un angle droit (90°) est \(\frac{\pi}{2}\) rad.
  
• La mesure en radians d'un angle plat (180°) est \(\pi\) rad.